Μεταφράζει ο Αλέξανδρος Τσαντίλας
Ο Charles Howard Hinton (1853 – 1907) ήταν Βρετανός μαθηματικός και συγγραφέας ιστοριών που κατατάσσονται στην πρώιμη περίοδο του λογοτεχνικού είδους της επιστημονικής φαντασίας.
Το έργο του αφορά την ύπαρξη και τη γεωμετρία των ανώτερων διαστάσεων, και o Hinton είναι ο πρώτος θεωρητικός της έννοιας της τέταρτης διάστασης που μελέτησε διεξοδικά τις ιδιότητες της με μαθηματικούς και επιστημονικούς όρους ∙ όπως είναι, επίσης, και ο πρώτος που δημιούργησε και χρησιμοποίησε την έννοια και τον όρο tesseract – «τεσσεράκτιο» ή «υπερκύβος», που αντιστοιχεί σ’ ένα θεωρητικό σχήμα τεσσάρων διαστάσεων το οποίο παρουσιάστηκε στο σύγγραμμα του με τίτλο A New Era of Thought του 1888.
Το δοκίμιο που παρουσιάζεται παρακάτω δημοσιεύτηκε για πρώτη φορά το 1884 με τη μορφή φυλλαδίου, όπως και τα υπόλοιπα δοκίμια και διηγήματα που συγκροτούν το βιβλίο του με τίτλο Scientific Romances.
Στην εποχή που βρισκόμαστε, οι ενέργειες μας επηρεάζονται σε πολύ μεγάλο βαθμό από τις θεωρίες μας. Έχουμε εγκαταλείψει τον απλό και ενστικτώδη τρόπο ζωής των προγενέστερων πολιτισμών για έναν τρόπο ζωής που ρυθμίζεται από τις πεποιθήσεις των γνώσεων μας και συμπληρώνεται από όλες τις επινοήσεις της νοημοσύνης. Σε μια τέτοια κατάσταση, μπορούμε να αναλογιστούμε ότι ενδέχεται να προκύψει κάποιος κίνδυνος, όχι μόνο από έλλειψη γνώσης και πρακτικών δεξιοτήτων, αλλά ακόμη κι απ’ το γεγονός ότι οι γνώσεις και οι πρακτικές δεξιότητες περιορίζονται σ’ έναν μοναχά τομέα, εάν υπάρχει έλλειψη πληροφόρησης σε άλλους τομείς. Εάν, λόγου χάρη, χρησιμοποιήσουμε την τωρινή μας γνώση περί των φυσικών νόμων και την δεξιότητα μας στον τομέα της μηχανικής, με σκοπό να χτίσουμε σπίτια δίχως να λαμβάνουμε υπόψη τις προϋποθέσεις που τίθενται από την φυσιολογία, είναι πολύ πιθανόν – μόνο και μόνο για να προσφέρουμε στους εαυτούς μας μια φαινομενική άνεση – να κάναμε τα σπίτια αυτά εντελώς αεροστεγή, έτσι που ακόμη και οι πιο καλά κατασκευασμένες επαύλεις να ήταν, στο εσωτερικό τους, γεμάτες με ασφυκτικά δωμάτια. Η γνώση του πώς είναι κατασκευασμένο το σώμα, καθώς και η γνώση των προϋποθέσεων της καλής του υγείας, μας αποτρέπουν απ’ το να προκαλούμε βλάβες σ’ αυτό καθώς επεκτείνουμε την κυριαρχία των δικών μας δυνάμεων επί της φύσης.
Με παρόμοιο τρόπο, η πνευματική ισορροπία του ανθρώπου προφυλάσσεται από τους κινδύνους της υπερβολικής προσήλωσης στους νόμους των επιστημών της μηχανικής μέσα από τον ορθό συλλογισμό του πώς συγκροτείται η ανθρώπινη γνωστική λειτουργία, και ποιες είναι οι προϋποθέσεις που απαιτεί η γνώση. Όποια κι αν είναι η επιδίωξη μας, ενεργούμε συνειδητά ή ασυνείδητα βάσει κάποιας θεωρίας, κάποιας οπτικής των πραγμάτων. Κι όταν τα όρια του καθημερινού τρόπου ζωής στενεύουν ολοένα και περισσότερο λόγω της συνεχώς αυξανόμενης πολυπλοκότητας του πολιτισμού μας, γίνεται δυο φορές σημαντικότερο να μοιραζόμαστε όχι μια μεμονωμένη σκέψη, αλλά κάθε σκέψη που μπορεί να έχουμε.
Δύο είναι οι οδοί για να μεταβούμε πέρα από την επικράτεια της πρακτικής σιγουριάς και να στρέψουμε τη ματιά μας στο αχανές εύρος των δυνατοτήτων. Ο ένας τρόπος είναι να αναρωτηθούμε: «Τί είναι γνώση; Τί αποτελεί εμπειρία;». Εάν υιοθετήσουμε αυτή την οδό, θα βυθιστούμε σ’ έναν ωκεανό υποθετικότητας. Εάν δεν διαθέταμε τα ανώτατα προσόντα του πνεύματος, που του επιτρέπουν να στοχάζεται όλη αυτή την απεραντοσύνη, θα επιστρέφαμε στο στέρεο έδαφος των τεκμηρίων, νιώθοντας μοναχά ένα αίσθημα ανακούφισης επειδή καταφέραμε να ξεφύγουμε απ’ όλη την σύγχυση και την αντιφατικότητα.
Η άλλη οδός, αυτή που μας οδηγεί πέρα από τον ορίζοντα του απτού βιώματος, είναι η αμφισβήτηση όλων όσων φαντάζουν περιορισμένα, με αυθαίρετο και παράλογο τρόπο, στην επικράτεια της γνώσης. Μια τέτοιου είδους αμφισβήτηση έχει συχνά, και με επιτυχία, εφαρμοστεί κατά την αναζήτηση νέων γνωστικών τεκμηρίων. Για πολύ μεγάλο χρονικό διάστημα, θεωρούσαμε ως δεδομένο ότι τέσσερα αέρια δεν μπορούσαν να μεταβούν σε υγρή κατάσταση. Μόνο πρόσφατα ήταν που ένας φυσικός απέδειξε, επιτυχώς, ότι δεν υφίσταται ουδεμία τέτοια αυθαίρετη διάκριση μεταξύ αερίων. Πρόσφατα, επίσης, το ερώτημα τέθηκε εκ νέου: «Υπάρχει, άραγε, μια τέταρτη κατάσταση της ύλης;». Γνωρίζουμε την στερεή, την υγρή, και την αέρια κατάσταση ∙ ο κύριος Κρουκς επιχειρεί να αποδείξει ότι υπάρχει μια κατάσταση διαφορετική από όλες αυτές. Ο σκοπός του κειμένου που αναπτύσσεται στις σελίδες αυτές είναι να δείξει ότι εάν φέρουμε στο νου ορισμένους περιορισμούς αναφορικά με τις θεμελιακές προϋποθέσεις της ύπαρξης όπως εμείς την γνωρίζουμε, το αποτέλεσμα θα είναι να συλλάβουμε μια κατάσταση ύπαρξης με δυνάμεις που υπερβαίνουν κατά πολύ τις δικές μας. Όταν αυτό το αποτέλεσμα καταστεί ξεκάθαρο, δεν θα ήταν καθόλου άτοπο να διερευνήσουμε το είδος των σχέσεων που ενδέχεται να υφίστανται μεταξύ του δικού μας τρόπου ύπαρξης, και εκείνου που δύναται να υπάρχει.
Οπότε, το ερώτημα που τίθεται ευθύς εξαρχής είναι: Ποιος είναι ο περιορισμός που οφείλουμε να στοχαστούμε;
Ένας παρατηρητής που στέκεται στην γωνία ενός δωματίου έχει τη δυνατότητα να επιλέξει, εκ φυσικού του, να κινηθεί προς τρεις κατευθύνσεις: προς τα επάνω, ακολουθώντας τη γραμμή όπου ενώνονται οι δύο τοίχοι ∙ προς τα εμπρός, εκεί όπου το πάτωμα ενώνεται με έναν από τους τοίχους ∙ και πλαγίως, εκεί όπου το πάτωμα ενώνεται με τον άλλο τοίχο. Μπορεί να προχωρήσει προς κάθε άλλο τμήμα του πατώματος του δωματίου αν κινηθεί ευθεία, παράλληλα με έναν τοίχο, κι έπειτα πραγματοποιήσει στροφή στις ορθές γωνίες, βαδίζοντας, αυτή τη φορά, παράλληλα με τον άλλο τοίχο. Στην περίπτωση αυτή, ο παρατηρητής πρώτα-πρώτα βαδίζει στην κατεύθυνση μιας από τις ευθείες γραμμές που ενώνονται στις γωνίες του πατώματος, κι έπειτα ακολουθεί την κατεύθυνση μιας από τις άλλες ευθείες. Αν κινηθεί τηρώντας, λίγο-πολύ, την μία ή την άλλη κατεύθυνση, μπορεί να φτάσει σε οποιοδήποτε σημείο του πατώματος, και κάθε του κίνηση, όσο κυκλική κι αν είναι, μπορεί να αναχθεί σε απλές κινήσεις προς τη μία, ή την άλλη, από τις δύο κατευθύνσεις αυτές.
Όμως, αν κινείται μόνο στις δύο αυτές κατευθύνσεις, είναι αδύνατον για τον παρατηρητή να στραφεί προς το επάνω τμήμα του δωματίου. Εάν επιθυμεί να ακουμπήσει ένα σημείο του ταβανιού, θα πρέπει να κινηθεί προς την κατεύθυνση της γραμμής όπου ενώνονται οι δύο τοίχοι. Κατά συνέπεια, οι κατευθύνσεις είναι τρεις, και η κάθε μια τους είναι μεν σε ορθή γωνία με τις άλλες, αλλά και εντελώς ανεξάρτητη από τις άλλες. Κινούμενος σε αυτές τις τρεις κατευθύνσεις, ή σε συνδυασμό τους, ο παρατηρητής μπορεί να μεταβεί σε οποιοδήποτε σημείο του δωματίου. Περαιτέρω, αν υποθέσουμε ότι οι ευθείες γραμμές που ενώνονται στην γωνία του δωματίου προεκτείνονται στο άπειρο, τότε αν ο παρατηρητής κινηθεί προς την κατεύθυνση μίας εκ των τριών γραμμών, μπορεί να φτάσει σε οποιοδήποτε σημείο του χώρου. Επομένως, στον χώρο υπάρχουν τρεις και μόνο τρεις ανεξάρτητες κατευθύνσεις: οποιαδήποτε άλλη κατεύθυνση δεν προκύπτει παρά μόνο ως συνδυασμός αυτών των τριών. Άρα, το ερώτημα με το οποίο ερχόμαστε αντιμέτωποι διαμορφώνεται ως εξής: «Γιατί υπάρχουν τρεις και μόνο τρεις κατευθύνσεις;». Ο χώρος, όπως εμείς τον αντιλαμβανόμαστε, διέπεται από έναν περιορισμό.
Προκειμένου να φτάσουμε σε μια επαρκή σύλληψη ως προς το ποιόν του παραπάνω περιορισμού, απαιτείται πρώτα να φανταστούμε κάποια όντα, που να διάγουν τον βίο τους σε έναν χώρο πολύ πιο περιορισμένο απ’ αυτόν στον οποίο κινούμαστε εμείς. Έτσι, μπορούμε να σχηματίσουμε στο νου μας ένα ον το οποίο, καθ’ όλο το εύρος των εμπειριών του, είναι περιορισμένο σε μία και μόνο ευθεία γραμμή. Το εν λόγω ον θα γνώριζε την κίνηση εμπρός και πίσω, αλλά τίποτε άλλο ∙ για εκείνο, ο χώρος ολάκερος δεν θα ήταν παρά η προέκταση των δύο κατευθύνσεων της ευθείας γραμμής προς μια άπειρη απόσταση. Είναι προφανές ότι δυο τέτοια πλάσματα ποτέ δεν θα περάσουν το ένα πλάι στο άλλο. Μπορούμε να φέρουμε στο μυαλό μας την έξοδο τους από την ευθεία γραμμή και την επανείσοδο τους σε αυτήν, αλλά εφόσον η κίνηση τους πάντοτε ακολουθεί μια ευθεία γραμμή, τα πλάσματα δεν θα μπορούσαν να εννοηθούν καμία άλλη κατεύθυνση κίνησης που θα είχε ως συνέπεια τη συνάντηση τους. Το μοναδικό σχήμα που θα μπορούσε να υφίσταται σε μια τέτοια μονοδιάστατη ύπαρξη είναι αυτό μιας πεπερασμένης ευθείας γραμμής. Ουδεμία άλλη διαφορά δεν θα υπήρχε, όσον αφορά τις μορφές ∙ ό, τι θα υπήρχε, δεν θα ήταν παρά μακρύτερες ή κοντύτερες ευθείες γραμμές.
Ας προχωρήσουμε ένα βήμα πιο πέρα, στην επικράτεια της αντιληπτής ύπαρξης. Έστω ότι υπάρχει ένα ον που περιορίζεται στην επιφάνεια ενός επιπέδου, και καθ’ όλο το εύρος της εμπειρίας του, ουδέποτε μετακινήθηκε προς τα επάνω ή προς τα κάτω, και παρέμεινε μόνο στο ένα αυτό επίπεδο. Σκεφτείτε, λόγου χάρη, κάποιο σχήμα, έναν κύκλο ή ένα ορθογώνιο, προικισμένο με τη δύναμη της αντίληψης: το ον αυτό, εάν κινηθεί στην επιφάνεια του επιπέδου στο οποίο έχει σχεδιαστεί, θα μπορεί να κινηθεί προς μια πληθώρα κατευθύνσεων ∙ όμως, ασχέτως του πόσο διαφορετικές μπορεί αν φαίνονται οι κατευθύνσεις, θα αποτελούν συνδυασμό δύο βασικών κατευθύνσεων που θα είναι σε ορθή γωνία η μία με την άλλη. Εφόσον η επιφάνεια του επιπέδου παραμείνει εξ ολοκλήρου οριζόντια, το ον δεν θα μπορεί να κινηθεί προς τις κατευθύνσεις που αποκαλούμε επάνω και κάτω. Ακόμη, είναι σημαντικό να παρατηρήσουμε πως το επίπεδο θα φαινόταν διαφορετικό για ένα πλάσμα που είναι περιορισμένο στο εσωτερικό του απ’ ότι θα φαινόταν σε εμάς. Στην σκέψη μας, ένα επίπεδο συνήθως διαθέτει μια άνω και μια κάτω πλευρά, επειδή κατανοούμε το επίπεδο μόνο ως προϊόν επαφής στερεών. Όμως, ένα πλάσμα που θα ζούσε όλη του την ύπαρξη περιορισμένο σ’ ένα επίπεδο, δεν θα είχε την παραμικρή ιδέα ότι στο επίπεδο που ζει υπάρχουν δύο πλευρές. Σ’ ένα επίπεδο υπάρχει μήκος, και υπάρχει πλάτος ∙ τίποτε άλλο. Εάν το πλάσμα εντός του επιπέδου γνωρίζει τις κατευθύνσεις του «επάνω» και του «κάτω», τότε έχει ήδη μεταβεί εκτός του επιπέδου.
Άρα, ένα πλάσμα υπό αυτές τις συνθήκες, μπορεί να συλλάβει τις έννοιες του επάνω και του κάτω, να ανακαλύψει μια κατεύθυνση που διαφέρει από εκείνες που έχει συνηθίσει, και με τις οποίες δεν έχει κανένα κοινό; Είναι προφανές ότι τίποτα στην άμεση εμπειρία του πλάσματος δεν θα του έδινε μια τέτοια ένδειξη. Μόνο μέσω του συλλογισμού, απ’ τη μεριά του, θα μπορούσε να φτάσει στην παραπάνω ιδέα. Εάν φανταζόταν ένα ον που περιορίζεται σε μία και μόνο ευθεία γραμμή, τότε θα συνειδητοποιούσε ότι και το ίδιο κινείται προς δυο κατευθύνσεις, ενώ το πλάσμα στην ευθεία γραμμή μπορεί να κινηθεί μόνο προς μια ∙ κι αφού φτάσει σ’ αυτόν τον συλλογισμό, θα μπορούσε έπειτα να αναρωτηθεί: «Γιατί όμως ο αριθμός των κατευθύνσεων περιορίζεται σε δύο; Γιατί να μην υπάρχουν τρεις;»
Ένα πλάσμα (εάν υπήρχε) που κινείται σε ένα επίπεδο θα ήταν σε πλεονεκτικότερη θέση απ’ ότι ένα πλάσμα που μπορεί να κινηθεί σε μια ευθεία γραμμή ∙ κι αυτό διότι σ’ ένα επίπεδο υπάρχει η πιθανότητα άπειρης ποικιλίας σχημάτων, και το ον που έχουμε φανταστεί, θα μπορούσε να έρθει σε επαφή με έναν άπειρο αριθμό άλλων όντων ∙ δεν θα περιορίζονταν, όπως το πλάσμα στην ευθεία γραμμή, σε μόνο ένα πλάσμα σε κάθε του πλευρά.
Είναι φανερό ότι μπορούμε να κάνουμε πολλών ειδών κατεργαριές σ’ ένα ον που περιορίζεται σ’ ένα επίπεδο ∙ για ένα ον, ας πούμε, σαν αυτό που βρίσκεται στο εσωτερικό ενός τετραγώνου, η μόνη έξοδος, σύμφωνα με την αντίληψη του, θα ήταν διαμέσου μίας από τις πλευρές του τετραγώνου. Εάν οι πλευρές είναι αδιαπέραστες, τότε το ον φυλακίζεται αμέσως στο τετράγωνο, δίχως να έχει τρόπο διαφυγής.
Η περίπτωση του όντος θα μας φανεί πιο γνώριμη εάν αναλογιστούμε πώς θα γινόταν αισθητή μια παρόμοια περίπτωση στην δική μας ύπαρξη. Το πλάσμα είναι κλεισμένο προς όλες τις κατευθύνσεις που γνωρίζει. Εάν ένας άνθρωπος είναι προς όλες τις κατευθύνσεις που γνωρίζει, τότε θα περιβάλλεται από τέσσερις τοίχους, ένα ταβάνι κι ένα πάτωμα. Ένα δισδιάστατο ον στο εσωτερικό ενός τετραγώνου θα ήταν στην ίδια ακριβώς περίσταση με εκείνη ενός ανθρώπου, εάν εκείνος βρεθεί σε ένα δωμάτιο δίχως άνοιγμα σε καμία από τις πλευρές του. Μπορούμε, λοιπόν, να σηκώσουμε το ον αυτό από το εσωτερικό του τετραγώνου και να το αποθέσουμε έξω από το τετράγωνο ∙ έτσι, το ον θα συνειδητοποιούσε ότι βρίσκεται έξω από το μέρος εγκλεισμού του, χωρίς να έχει διασχίσει κάποιο από τα όρια που του έφραζαν κάθε οδό διαφυγής. Μπορούμε να διανοηθούμε την κατάπληξη που θα ένιωθε το ον αυτό, αν τη συγκρίνουμε με εκείνη που θα ένιωθε ο άνθρωπος, στην περίπτωση που θα έβρισκε ξαφνικά τον εαυτό του έξω από το δωμάτιο όπου ήταν κλεισμένος, χωρίς να έχει περάσει ούτε μέσα από το παράθυρο, ούτε μέσα από την πόρτα, ούτε από την καμινάδα, ούτε απ’ οποιοδήποτε άλλο άνοιγμα στους τοίχους, το ταβάνι ή το πάτωμα.
Ένα ακόμη παράξενο πράγμα που θα μπορούσε να συμβεί σ’ ένα δισδιάστατο πλάσμα έχει ως εξής: φανταστείτε δύο όντα που βρίσκονται σε μεγάλη απόσταση το ένα από το άλλο σε μια επίπεδη επιφάνεια. Εάν η επίπεδη επιφάνεια καμπυλωθεί, έτσι που το ένα ον να φτάσει κοντά στο άλλο, τα δύο όντα δεν θα είχαν καμία συναίσθηση της μεταξύ τους εγγύτητας, δεδομένου ότι το κάθε ένα από αυτά θα αντιλαμβανόταν την κίνηση μόνο ως κίνηση στην επιφάνεια. Τα δυο όντα θα μπορούσαν να τοποθετηθούν σε μια τέτοια θέση μεταξύ τους, μέσω μιας καμπύλωσης του επιπέδου, έτσι ώστε να έρθουν πλάι-πλάι το ένα με το άλλο, και σε κάθε περίπτωση, η λογική τους θα τους έλεγε ότι μεταξύ τους παρεμβαίνει μια μεγάλη απόσταση. Εάν το επίπεδο καμπυλωθεί σε μεγαλύτερο ακόμη βαθμό, το ένα ον θα εμφανιστεί από το πουθενά πλάι στο άλλο. Εάν τα όντα αυτά αγνοούν την ύπαρξη μιας τρίτης διάστασης, το αποτέλεσμα θα τους φαινόταν άκρως υπερφυσικό ∙ όπως, εξάλλου, θα φαινόταν κι αν συνέβαινε σε έναν άνθρωπο που, τη μια στιγμή θα ήταν σε μακρινή απόσταση – ακόμη και στην άλλη άκρη του κόσμου – και την άλλη στιγμή θα εμφανιζόταν ξαφνικά δίπλα μας, ενώ καθ’ όλη τη διάρκεια της μετάβασης, δεν θα είχε καθόλου μετακινηθεί απ’ το σημείο στο οποίο βρισκόταν.
Τα προηγούμενα παραδείγματα δείχνουν ξεκάθαρα ότι μπορούμε να φανταστούμε όντα που ζουν σε έναν πιο περιορισμένο χώρο απ’ ότι εμείς. Άρα, θα μπορούσε να υπάρχει ένας παρόμοιος περιορισμός στον χώρο που εμείς αντιλαμβανόμαστε;
Ερχόμαστε αντιμέτωποι μ’ έναν περιορισμό παρόμοιας φύσεως στο κατώφλι της ίδιας της αριθμητικής.
Εάν ενώπιον μας υπάρχει μια ευθεία γραμμή δύο ίντσες μακριά, το μήκος της εκφράζεται με τον αριθμό 2. Έστω ότι στη γραμμή περιγράφεται ένα τετράγωνο, έτσι που ο αριθμός των τετραγωνικών ιντσών του σχήματος να εκφράζεται με τον αριθμό 4, δηλαδή 2 × 2. Αυτό το 2 × 2 γενικά γράφεται ως 2^2 και ονομάζεται «2 εις το τετράγωνο».
Βέβαια, όπως είναι φυσικό, η αριθμητική διαδικασία του πολλαπλασιασμού δεν μοιάζει καθόλου με την διαδικασία παραγωγής ενός τετραγώνου από την κίνηση της ευθείας γραμμής, ή ενός κύβου από την κίνηση ενός τετραγώνου. Έχει, παρ’ όλα αυτά, παρατηρηθεί οι οι μονάδες που προκύπτουν από αμφότερες τις περιπτώσεις, μολονότι διαφέρουν ως προς το είδος τους, είναι ίδιες σε αριθμό.
Αν αγγίξουμε δύο πράγματα δύο φορές, τότε η ενέργεια της αφής έχει τελεστεί τέσσερις φορές. Αριθμητικά μιλώντας, 2 × 2 = 4. Εάν ένα τετράγωνο παράγεται από την κίνηση μιας γραμμής μήκους δυο ιντσών, τότε το τετράγωνο αυτό περιέχει τέσσερις τετραγωνικές ίντσες.
Οπότε, η δεύτερη και η τρίτη δύναμη των αριθμών καλούνται «τετράγωνο» και «κύβος», αντίστοιχα.
Τώρα, έχουμε μια ευθεία γραμμή δύο ίντσες μακριά. Σε αυτήν κατασκευάζεται ένα τετράγωνο που περιέχει τέσσερις τετραγωνικές ίντσες. Εάν στην ίδια γραμμή κατασκευαστεί ένας κύβος, τότε ο αριθμός των κυβικών ιντσών του σχηματιζόμενου σχήματος θα είναι 8, δηλαδή 2 × 2 × 2 ή 2^3. Στο σημείο αυτό, κατ’ αντιστοιχία με τους αριθμούς 2, 2^2, 2^3, έχουμε μια σειρά σχημάτων. Κάθε σχήμα περιέχει περισσότερες μονάδες απ’ ότι το αμέσως προηγούμενο του, και σε κάθε ένα σχήμα η μονάδα είναι διαφορετικού είδους. Στο πρώτο σχήμα, η μονάδα είναι η ευθεία γραμμή, δηλαδή μια γραμμική ίντσα ∙ σε αυτή την περίπτωση, λέμε ότι το σχήμα αυτό διαθέτει μία μόνο διάσταση. Στο δεύτερο σχήμα, η μονάδα είναι το τετράγωνο, δηλαδή μία τετραγωνική ίντσα ∙ λέμε, αντίστοιχα, ότι το τετράγωνο αποτελεί σχήμα δύο διαστάσεων. Στην τρίτη περίπτωση, η μονάδα είναι ο κύβος, και ο κύβος διαθέτει τρεις διαστάσεις. Η ευθεία γραμμή θεωρείται μονοδιάστατη διότι μετριέται με έναν μόνο τρόπο ∙ μπορεί να υπολογιστεί το μήκος της, αλλά δεν διαθέτει ούτε πλάτο, ούτε πάχος. Το τετράγωνο θεωρείται δισδιάστατο λόγω του ότι διαθέτει και μήκος, και πλάτος. Ο κύβος καλείται τρισδιάστατος επειδή μπορεί να μετρηθεί με τρεις τρόπους.
Κοιτάζοντας τους αριθμούς 2, 2^2, 2^3, το ερώτημα που προκύπτει με φυσικό τρόπο είναι με ποιο σχήμα θα αναπαραστήσουμε το 2^4, ή 2 × 2 × 2 × 2. Γνωρίζουμε ότι στο σχήμα θα πρέπει να υπάρχουν δεκαέξι μονάδες, ή τις διπλάσιες μονάδες από αυτές που υπάρχουν στον κύβο. Ωστόσο, η μονάδα αυτή καθ’ αυτή θα πρέπει επίσης να είναι διαφορετική, αλλά κι ότι δεν θα πρέπει να διαφέρει από έναν κύβο μοναχά όσον αφορά το σχήμα ∙ θα πρέπει να διαφέρει από έναν κύβο όσο ένας κύβος διαφέρει από ένα τετράγωνο. Ένας κύβος δεν μπορεί να συγκροτηθεί από τετράγωνα, όσα πολλά κι αν είναι αυτά, επειδή το τετράγωνο, ως σχήμα, δεν διαθέτει πάχος. Με παρόμοιο τρόπο, η νέα μονάδα δεν δύναται να συγκροτηθεί από έναν αριθμό κύβων. Οπότε, έχοντας φτάσει στο σημείο αυτό, αντί να προσπαθούμε να βρούμε κάτι ήδη γνωστό, κάτι στο οποίο θα μπορεί να προσαρτηθεί η ιδέα του σχήματος που θα αντιστοιχεί στην τέταρτη δύναμη, ας συλλογιστούμε απλά ποιες θα πρέπει να είναι οι ιδιότητες ενός τέτοιου σχήματος. Σε αυτή μας την απόπειρα θα πρέπει να βασιστούμε όχι σε μια διαδικασία αφής ή όρασης, που μας κατατοπίζουν για τις ιδιότητες των σωμάτων στον χώρο που αντιλαμβανόμαστε, αλλά σε μια διαδικασία σκέψης. Κάθε πληροφορία περί αυτού του αγνώστου σχήματος θα πρέπει να αναλυθεί λογικά με διεξοδικό τρόπο, και μόνο αφού ολοκληρωθούν ορισμένα συλλογιστικά βήματα θα μας δοθεί η δυνατότητα να καταλήξουμε σε κάποιο γνώριμο συμπέρασμα σχετικά με τις ιδιότητες του, έτσι που να μην υποπίπτουμε σε ανακολουθίες. Απ’ όλες τις εφαρμογές της λογικής, αυτή η διερεύνηση είναι ίσως η μοναδική που απαιτεί – λόγω της απλότητας των δεδομένων που περιλαμβάνονται σε αυτήν – την μεγαλύτερη άσκηση της φαντασίας στην πιο αφηρημένη της μορφή ∙ απ’ αυτή την άποψη, αξίζει την προσοχή και την υπομονή μας. Τα πρώτα βήματα είναι πολύ απλά: πρέπει να φανταστούμε μια πεπερασμένη ευθεία γραμμή προκειμένου να παράγουμε ένα τετράγωνο μέσω της κίνησης στο επίπεδο του χαρτιού, κι έπειτα, από το τετράγωνο αυτό να παράγουμε έναν κύβο κινούμενοι κάθετα προς τα επάνω. Το σχήμα 1 αναπαριστά μια ευθεία γραμμή∙ το σχήμα 2 αναπαριστά ένα τετράγωνο που σχηματίζεται από την κίνηση αυτής της ευθείας γραμμής ∙ και το σχήμα 3, αντίστοιχα, αναπαριστά έναν κύβο που σχηματίζεται από την κίνηση του τετραγώνου ΑΒΓΔ προς τα επάνω. Αντί να χρησιμοποιήσουμε το σχήμα 3, μπορούμε κάλλιστα να τοποθετήσουμε έναν κύβο επάνω στο χαρτί. Η βάση του κύβου θα αντιστοιχούσε στο τετράγωνο ΑΒΓΔ, ενώ η επάνω επιφάνεια του κύβου θα ήταν το τετράγωνο ΕΖΗΘ.
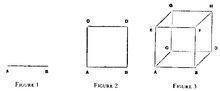
Όσον αφορά το σχήμα ΑΒΓΔ, υπάρχει η δυνατότητα κίνησης σε διαφορετικές κατευθύνσεις, αν και εφόσον οι κατευθύνσεις αυτές περιορίζονται σε ένα επίπεδο. Το σύνολο των κατευθύνσεων στο επίπεδο μπορούν να θεωρηθούν ως συνδυασμοί δύο βασικών κατευθύνσεων: από το Α στο Β, κι από το Α στο Γ. Από το άπειρο πλήθος κατευθύνσεων τέτοιου είδους, καμία δεν τείνει προς μια κατεύθυνση κάθετα προς το σχήμα 2 – δηλαδή καμία δεν τείνει προς το επάνω τμήμα του επιπέδου στο χαρτί. Φανταστείτε ένα ον που ζει και κινείται μόνο εντός των ορίων του επιπέδου: καμία απ’ τις κινήσεις που θα έκανε δεν θα το οδηγούσε στη σύλληψη της μεταβολή του σχήματος 2 σε αυτό που αναπαριστά οπτικά το σχήμα 3. Διότι, για να προκύψει το σχήμα 3 από το σχήμα 2, θα πρέπει να υποτεθεί μια κάθετη κίνηση προς το επίπεδο του σχήματος 2. Το σχήμα που θα χαραχτεί θα είναι ο κύβος ΑΒΓΔΕΖΗΘ.
Όλες οι κατευθύνσεις, όσο πολυάριθμες κι αν είναι, που θα μπορούσε να ακολουθήσει ένα πλάσμα που ζει στο σχήμα 3, είναι συνδυασμοί τριών κατευθύνσεων: από το Α στο Β, από το Α στο Γ, κι από το Α στο Ε. Το πλάσμα δεν θα αντιλαμβανόταν καμία άλλη κίνηση.
Όμως, εάν στο σχήμα 3 συμβεί κάτι παρόμοιο με αυτό που συνέβη στο σχήμα 1 και το μετέτρεψε στο σχήμα 2, ή με αυτό που συνέβη στο σχήμα 2 που μετατράπηκε στο σχήμα 3, τότε θα θεωρήσουμε ότι το συνολικό σχήμα, όπως αυτό υφίσταται, μετακινήθηκε προς κάποια κατεύθυνση εξ ολοκλήρου διαφορετική έναντι οποιασδήποτε άλλης κατεύθυνσης στο εσωτερικό του που, μεταξύ άλλων, δεν συνίστανται από έναν συνδυασμό των ήδη αναγνωρισμένων κατευθύνσεων του. Σε τι αντιστοιχεί το παραπάνω; Αντιστοιχεί στην τέταρτη διάσταση.
Ο νους μας αδυνατεί να τη φανταστεί, όπως ένα πλάσμα που ζει στο επίπεδο σχήμα 2 θα αδυνατούσε να φανταστεί μια κατεύθυνση που, κινούμενο εντός αυτής, το τετράγωνο 2 θα μετατρέπονταν στον κύβο 3. Σ’ ένα τέτοιο πλάσμα, η τρίτη διάσταση θα φάνταζε εξίσου ακατάληπτη όσο και φαίνεται και η τέταρτη διάσταση σε εμάς. Στο σημείο αυτό, αναγκαζόμαστε να εγκαταλείψουμε κάθε βοήθημα που θα μας δινόταν από ορατά αντικείμενα, κι απλά προχωράμε στην διερεύνηση των ιδιοτήτων του πιο απλού σχήματος σε τέσσερις διαστάσεις. Για τη διερεύνηση αυτή, ακολουθούμε τους κανόνες της αναλογίας που γνωρίζουμε ότι υπάρχει ανάμεσα στην διαδικασία σχηματισμού του σχήματος 2 από το σχήμα 1, του σχήματος 3 από το 2, κι εντέλει, του σχήματος 4 από το 3. Χάριν ευκολίας, ας ονομάσουμε το σχήμα που διερευνούμε – το πιο απλό σχήμα τεσσάρων διαστάσεων – ως τετράκις-τετράγωνο.
Πρώτα απ’ όλα, θα παρατηρήσουμε ότι εάν ένας κύβος σχηματίζεται από ένα τετράγωνο μέσω της κίνησης του τετραγώνου προς μια καινούργια κατεύθυνση, τότε κάθε σημείο στο εσωτερικό του τετραγώνου χαράσσει κι από ένα τμήμα του κύβου. Ο κύβος δεν σχηματίζεται μόνο από τις κινήσεις των γραμμών στα όρια ∙ κάθε τμήμα εντός του τετραγώνου παράγει κι από ένα τμήμα του κύβου. Άρα, εάν ένας κύβος κινηθεί προς την τέταρτη διάσταση, δημιουργώντας, μέσω της κίνησης του, ένα τετράκις-τετράγωνο, τότε κάθε σημείο στο εσωτερικό του κύβου θα ξεκινούσε εκ νέου, χαράσσοντας ένα τμήμα του νέου σχήματος, δίχως να συναντά κάποιο από τα υπόλοιπα σημεία.
Ας δούμε το ζήτημα υπό άλλο πρίσμα: αν ένα ον τριών διαστάσεων, κοιτάξει ένα τετράγωνο από επάνω, τότε βλέπει μπροστά του να εκτείνεται κάθε τμήμα του τετραγώνου, και μπορεί να αγγίξει κάθε τμήμα χωρίς να χρειάζεται να διασχίσει κάποιο από τα τμήματα που το περιβάλλουν, διότι η κίνηση του γίνεται από ψηλά, ενώ τα γύρω τμήματα περιβάλλουν μόνο ένα επίπεδο του τμήματος που αγγίζεται από το ον.
Κατ’ αυτό τον τρόπο, ένα ον σε τέσσερις διαστάσεις μπορεί να δει και να αγγίξει οποιοδήποτε σημείο ενός στερεού σχήματος. Κανένα τμήμα δεν θα μπορούσε να αποκρύψει κάποιο άλλο, διότι το ον αυτό θα κοίταζε κάθε τμήμα από μια κατεύθυνση ολωσδιόλου διαφορετική από εκείνες που επιτρέπουν τη διέλευση από ένα τμήμα του σώματος σ’ ένα άλλο. Η μετάβαση από ένα τμήμα του σώματος σ’ ένα άλλο απαιτεί κίνηση σε τρεις κατευθύνσεις ∙ ένα ον σε τέσσερις διαστάσεις, ωστόσο, θα έβλεπε το στερεό από μια κατεύθυνση που δεν αντιστοιχεί σε καμία από τις τρεις αυτές κατευθύνσεις.
Ας συμπεράνουμε ορισμένα στοιχεία σχετικά με το τέταρτο σχήμα, τηρώντας την αναλογία που γνωρίζουμε ότι υφίσταται μεταξύ των 1, 2, 3, και 4. Στο σχήμα 1 υπάρχουν δύο σημεία ∙ στο σχήμα 2, τέσσερα – τα σημεία που αντιστοιχούν στις τέσσερις γωνίες του τετραγώνου. Στο σχήμα 3, αντίστοιχα, υπάρχουν οκτώ σημεία. Στο επόμενο σχήμα, ακολουθώντας τον ίδιο νόμο, θα υπάρχουν δεκαέξι σημεία.
Στο σχήμα 1 υπάρχει μία μόνο γραμμή. Στο τετράγωνο υπάρχουν τέσσερις γραμμές ∙ στον κύβο, δώδεκα. Πόσες γραμμές θα έχει το τετράκις τετράγωνο; Με άλλα λόγια, μέχρι στιγμής υπάρχουν τρεις αριθμοί: οι αριθμοί 1, 4, και 12. Ποιος είναι ο τέταρτος αριθμός που προκύπτει, σύμφωνα με τον ίδιο νόμο;
Για να δώσουμε απάντηση στο ερώτημα αυτό, ας αναλύσουμε λεπτομερώς τον τρόπο με τον οποίο τα σχήματα μεταβάλλονται, παίρνοντας το ένα τη μορφή τους του άλλου. Η γραμμή, για να γίνει τετράγωνο, κινείται ∙ καταλαμβάνει, αρχικά, την αρχική της θέση, κι εντέλει, την τελική της θέση. Ξεκινάει ως ΑΒ και καταλήγει ως ΓΔ ∙ άρα, η γραμμή εμφανίζεται εις διπλούν, ή διπλασιάζεται. Οι άλλες δύο γραμμές του τετραγώνου, οι ΑΓ και ΒΔ, σχηματίζονται από τις κινήσεις των σημείων στα άκρα της κινούμενης γραμμής. Συνεπώς, κατά τη μετάβαση από την ευθεία γραμμή στο τετράγωνο, οι γραμμές διπλασιάζονται, έτσι που κάθε σημείο να χαράσσει κι από μια γραμμή. Εάν ισχύει η ίδια διαδικασία στην περίπτωση της μεταβολής του τετραγώνου σε κύβο, τότε στην περίπτωση του κύβου θα πρέπει να διπλασιάσουμε τον αριθμό των γραμμών όπως και στο τετράγωνο – δηλαδή να τις κάνουμε οκτώ – και κάθε σημείο του τετραγώνου θα πρέπει να μετατραπεί σε μία γραμμή. Αφού υπάρχουν τέσσερα σημεία στο τετράγωνο, θα πρέπει εξ αυτών να έχουμε τέσσερις γραμμές στον κύβο∙ πράγμα που σημαίνει ότι αν προσθέσουμε και τις προηγούμενες οκτώ, τότε ο κύβος θα διαθέτει δώδεκα γραμμές – όπως βλέπουμε να συμβαίνει. Ως εκ τούτου, για να εξακριβώσουμε τον αριθμό των γραμμών σε ένα τετράκις τετράγωνο, μπορούμε, δίχως δισταγμούς, να εφαρμόσουμε τον κανόνα που αναλύθηκε πιο πριν: για να βρούμε πόσες γραμμές θα υπάρχουν, διπλασιάζουμε τον αριθμό των γραμμών του προηγούμενου σχήματος, και προσθέτουμε τόσες γραμμές όσα και τα σημεία στο προηγούμενο σχήμα. Ο κύβος έχει δώδεκα γραμμές και οκτώ σημεία: άρα, έχουμε 2 × 12 + 8, ή αλλιώς, τριανταδύο γραμμές στο τετράκις τετράγωνο.
Με παρόμοιο τρόπο μπορούμε να απαντήσουμε κάθε ερώτημα περί του τετράκις τετραγώνου. Πρέπει να παραμερίσουμε την αντιληπτική μας ικανότητα και να απαντάμε σύμφωνα με την αναλογία που διαπιστώσαμε ότι υπάρχει από τα άλλα τρία σχήματα που γνωρίζουμε.
Επομένως, αν θέλουμε να μάθουμε πόσες επίπεδες επιφάνειες διαθέτει το τετράκις τετράγωνο, θα πάρουμε ως αφετηρία μας τη γραμμή, που δεν διαθέτει καμία επίπεδη επιφάνεια ∙ το τετράγωνο, με τη σειρά του, έχει μια ∙ ο κύβος, έξι. Εδώ καταλήγουμε στους αριθμούς 0, 1 και 6. Ποιος είναι ο τέταρτος αριθμός;
Σκεφτείτε με ποιο τρόπο προκύπτουν τα επίπεδα του κύβου. Το τετράγωνο, κατά την αφετηρία της κίνησης του, προσδιορίζει μία από τις όψεις του κύβου, και στο τέλος της κίνησης καταλήγει στην αντίθετη όψη, ενώ κατά την κίνηση, κάθε μία απ’ τις γραμμές του τετραγώνου χαράσσει κι από μια επίπεδη όψη του κύβου. Άρα, διπλασιάζουμε τον αριθμό των επιπέδων του προηγούμενου σχήματος, και κάθε γραμμή του προηγούμενου σχήματος χαράσσει κι από ένα επίπεδο του επακόλουθου σχήματος.
Ας εφαρμόσουμε τον κανόνα αυτό κατά τον σχηματισμό ενός τετραγώνου από μία γραμμή. Στην γραμμή δεν υπάρχει καμία επίπεδη επιφάνεια, κι εφόσον δύο επί μηδέν ισούται με μηδέν, μέχρις εδώ δεν καταλήγουμε με καμία επιφάνεια στο τετράγωνο ∙ στην ευθεία γραμμή, όμως, υπάρχει μία γραμμή, η ίδια η γραμμή της ευθείας, και με την κίνηση της χαράσσει την επίπεδη επιφάνεια του τετραγώνου. Οπότε, στο τετράγωνο, όπως είναι αναμενόμενο, ο κανόνας μας δίνει μία επιφάνεια.
Αν εφαρμόσουμε τον ίδιο κανόνα στην περίπτωση του κύβου, τότε ο διπλασιασμός των επιφανειών μας δίνει ως αποτέλεσμα τον αριθμό 12. Αν, έπειτα, προσθέσουμε ένα επίπεδο για κάθε μία απ’ τις ευθείες γραμμές, που ο αριθμός τους είναι 12, καταλήγουμε με άλλες 12 ∙ στο σύνολο τους, 24 επίπεδες επιφάνειες. Συνεπώς, η ενασχόληση, ή έστω και με μία μόνο ματιά ενός σχήματος στο χώρο, μας επιτρέπει να περιγράψουμε το σχήμα ∙ οπότε, μέσω μιας διαδικασίας υπολογισμού, μας δίνεται η δυνατότητα να περιγράψουμε όλες τις ιδιότητες ενός σχήματος σε τέσσερις διαστάσεις.
Υπάρχει ένα ακόμη χαρακτηριστικό, τόσο αξιοθαύμαστο ώστε να απαιτεί ειδική περιγραφή: τα σύνορα μίας πεπερασμένης ευθείας γραμμής αντιστοιχούν σε σημεία. Εάν έχουμε να κάνουμε μόνο με μία διάσταση, τότε το σχήμα 1, που αποτελεί ευθύγραμμο τμήμα της γραμμής, τεμαχίζεται και διαχωρίζεται από το υπόλοιπο τμήμα μιας νοητής ευθείας γραμμής, άπειρης σε μήκος, μέσω των δύο σημείων στα άκρα του. Στην απλή αυτή περίπτωση, τα δύο σημεία αντιστοιχούν στην συνοριακή επιφάνεια του κύβου. Στην περίπτωση ενός δισδιάστατου σχήματος, ο συνολικός χώρος αναπαρίσταται από ένα άπειρο επίπεδο. Το τετράγωνο διαχωρίζεται από το υπόλοιπο επίπεδο χάρη σε τέσσερις ευθείες γραμμές, και είναι αδύνατο να υπάρξει οποιαδήποτε είσοδος στο εσωτερικό του τετραγώνου, εκτός κι αν διασχίσουμε τις ευθείες γραμμές. Στις παραπάνω περιπτώσεις, είναι φανερό ότι τα σύνορα του σχήματος αποτελούνται από μια διάσταση λιγότερο απ’ ότι το ίδιο το σχήμα. Τα σημεία φράσσουν τις γραμμές, οι γραμμές φράσσουν τα επίπεδα σχήματα, και τα επίπεδα φράσσουν τα στερεά. Επομένως, τα τετραδιάστατα σχήματα θα πρέπει, με τη σειρά τους, να φράσσονται από τα στερεά.
Το τετράκις τετράγωνο θα φράσσεται ως εξής: πρώτον, υπάρχει ένας κύβος, και η κίνηση του κύβου προς την τέταρτη διάσταση έχει ως αποτέλεσμα την παραγωγή του σχήματος. Ο κύβος αυτός, στην αρχική του θέση, σχηματίζει τη βάση του τετράκις τετραγώνου, ενώ στην τελική του θέση σχηματίζει την αντίθετη όψη της βάσης. Κατά την κίνηση, από κάθε μία από τις όψεις του κύβου προκύπτει ένας ακόμη κύβος. Η κατεύθυνση προς την οποία κινείται ο κύβος είναι τέτοια που, απ’ όλες τις έξι πλευρές, καμία τους να μην κλίνει προς την κατεύθυνση της κίνησης ούτε καν στο ελάχιστο, και κάθε μία πλευρά θα είναι σε ορθή γωνία προς όλες τις υπόλοιπες. Η βάση του κύβου, η κορυφή του κύβου, και οι τέσσερις πλευρές του κύβου, όλες τους μαζί, και κάθε μία ξεχωριστά, σχηματίζουν άλλους κύβους. Ως εκ τούτου, το τετράκις τετράγωνο φράσσεται από οκτώ κύβους. Αθροιστικά, το τετράκις τετράγωνο διαθέτει 16 σημεία, 32 γραμμές, 24 επιφάνειες, και θα φράσσεται από 8 κύβους.
Εάν ένα τετράκις τετράγωνο ακουμπούσε στον χώρο μας, θα το βλέπαμε σαν κύβο.
Για να δικαιολογήσουμε το παραπάνω συμπέρασμα, δεν έχουμε παρά να αναλογιστούμε πώς θα φαινόταν ένας κύβος σ’ ένα δισδιάστατο ον. Για να μπορέσει έστω να εισέλθει εντός του πεδίου της αντίληψης του, θα πρέπει να έρθει σε επαφή με το επίπεδο στο οποίο το ον κινείται. Εάν έρθει σε όσο το δυνατόν εγγύτερη επαφή με το επίπεδο, τότε μία από τις όψεις του κύβου θα ακουμπήσει στο επίπεδο ∙ η όψη αυτή αντιστοιχεί σε τετράγωνο, άρα αυτό που θα αντιλαμβανόταν το δισδιάστατο ον δεν θα ήταν, στην καλύτερη των περιπτώσεων, παρά ένα τετράγωνο.
Κατά συνέπεια, έχοντας διαπιστώσει ότι μπορούμε να περιγράψουμε τις ιδιότητες πιο απλού σχήματος σε τέσσερις διαστάσεις, βλέπουμε τώρα ότι η νοητική κατασκευή πιο περίπλοκων σχημάτων δεν είναι παρά θέμα χρόνου και υπομονής.
Κατά τη μελέτη της διαμόρφωσης και ανάπτυξης του νεοσσού μέσα στο αυγό, είναι αδύνατο να διακρίνουμε τα χαρακτηριστικά που θέλουμε να παρατηρήσουμε, εκτός κι αν χρησιμοποιήσουμε ένα μικροσκόπιο. Ακολούθως, τα εξεταζόμενα δείγματα περνάνε από μια περίεργη επεξεργασία σκλήρυνσης και κόβονται σε λεπτές τομές. Ο ερευνητής, έπειτα, εξετάζει κάθε μία απ’ αυτές τις τομές, σημειώνει όλες τις ιδιαιτερότητες τους, και κατασκευάζει νοερά το σχήμα του νεοσσού σύμφωνα με την πρότερη της μορφή από τα στοιχεία που δίνονται από τον εκάστοτε αριθμό τομών. Ως εκ τούτου, για να σχηματίσουμε μια ιδέα περί της μορφής που θα έχει ένα τετραδιάστατο σχήμα, θα πρέπει να αποτυπώσουμε στη σκέψη μας μια σειρά στερεών μορφών, που κάθε πλευρά τους φράσσεται, και που διαφέρουν βαθμιαία μεταξύ τους, προχωρώντας, ενδεχομένως, στον σχηματισμό των πιο ανόμοιων και ποικίλων μορφών ∙ και μετά, θα πρέπει να ενώσουμε τη σειρά αυτή σε ένα ενιαίο νοητό σχέδιο.
Εάν, λόγου χάρη, εμφανιζόταν μια μικρή σφαίρα, και αυτή την αντικαθιστούσε μια πιο μεγάλη, και μετά μια ακόμη μεγαλύτερη, και ούτω καθεξής, η εμφάνιση της μεγαλύτερης σφαίρας θα συνοδευόταν από την εμφάνιση σφαιρών που θα ήταν η μία πιο μικρή από την προηγούμενη ∙ κι αυτό θα αντιστοιχούσε σε μια σειρά τομών μιας τετραδιάστατης σφαίρας – και κάθε τομή της σφαίρας στον χώρο θα ήταν μια σφαίρα από μόνη της.
Ας επαναλάβουμε για μια ακόμη φορά ότι με τον ίδιο τρόπο που μπορούμε να αναπαραστήσουμε στέρεα σχήματα στο χαρτί μέσω της προοπτικής, έτσι ακριβώς μπορούμε να αναπαραστήσουμε και τετραδιάστατα σχήματα από στερεά. Εάν έχουμε δύο τετράγωνα, με το ένα να επικαλύπτει το άλλο, και σπρώξουμε το τετράγωνο στην κάτω μεριά μετακινώντας το, οι πλευρές του τετραγώνου θα συνεχίσουν να είναι παράλληλες με εκείνες του από επάνω τετραγώνου. Έτσι, αν κάθε σημείο του ενός τετραγώνου ενωθεί με το αντίστοιχο σημείο του άλλου, το αποτέλεσμα θα είναι μια λίγο-πολύ ακριβής αναπαράσταση ενός κύβου στο χαρτί. Το σχήμα 3 μπορεί να θεωρηθεί ότι αποτελεί μια τέτοια αναπαράσταση, αν θεωρήσουμε ότι το τετράγωνο ΓΔΕΖ είναι το τετράγωνο που σπρώχνεται μακριά από την αρχική του θέση, κάτω από το ΑΒΓΔ. Κάθε ένα από τα επίπεδα που φράσσουν τον κύβο αναπαρίσταται στο χαρτί ∙ το μόνο που υπολείπεται είναι το τρισδιάστατο περιεχόμενο του κύβου. Συνεπώς, αν δύο κύβοι τοποθετηθούν με τις πλευρές τους παράλληλα, αλλά με τον ένα κύβο τοποθετημένο κάπως διαγώνια πάνω στον άλλο, και όλα τα αντίστοιχα τους σημεία ενωθούν υποθετικά, τότε αυτό που θα προκύψει θα είναι ένα σύνολο στέρεων σχημάτων, με το κάθε ένα από αυτά να αναπαριστά (μολονότι, για να λέμε την αλήθεια, κάπως στρεβλά) τους κύβους που φράσσουν το τετραδιάστατο σχήμα, ενώ την ίδια στιγμή, η αναπαράσταση κάθε επιπέδου και γραμμής στο τετραδιάστατο σχήμα, θα φαίνεται να έχει προοπτική που προσεγγίζει τα στερεά. Αυτό που θα υπολείπεται είναι – φυσικά – το τετραδιάστατο περιεχόμενο.
Έχοντας πλέον εξετάσει μερικές από τις ιδιότητες των τετραδιάστατων σχημάτων, μένει να αναρωτηθούμε ποιες θα ήταν οι σχέσεις θα είχαν τα όντα σε τέσσερις διαστάσεις, εάν υπήρχαν, με εμάς.
Ας μην παραβλέπουμε, άλλωστε, ότι ένα ον σε τέσσερις διαστάσεις θα μας φαινόταν όπως ακριβώς ένα ον στον χώρο ∙ το ον σ’ ένα επίπεδο θα αναγνώριζε τα στέρεα αντικείμενα ως δισδιάστατα σχήματα – και πιο συγκεκριμένα, θα τα έβλεπε με τα σχήματα που θα είχαν καθώς θα έτεμναν το επίπεδο του. Έτσι, αν υπήρχαν τετραδιάστατα αντικείμενα, εμείς θα τα βλέπαμε μόνο ως στερεά – και πιο συγκεκριμένα, τα στερεά μέσω των οποίων θα έτεμναν τον χώρο μας. Επομένως, γιατί να μην θεωρήσουμε ότι εμείς οι ίδιοι είμαστε τα τετραδιάστατα όντα, κι ότι οι διαδοχικές μας καταστάσεις αντιστοιχούν στη μετάβαση τους, καθώς διασχίζουν τον τρισδιάστατο χώρο στον οποίο περιορίζεται η συνείδηση μας;
Ας σκεφτούμε πιο ενδελεχώς το ζήτημα – και χάριν ευκολίας, αντί για τις τέσσερις και τις τρεις διαστάσεις, ας μεταφέρουμε το πρόβλημα στην περίπτωση των τριών και των δύο διαστάσεων.
Έστω μια κλωστή που διαπερνά ένα λεπτό φύλλο κεριού τοποθετημένο οριζόντια. Το φύλλο μπορεί να διαπεραστεί με δύο τρόπους: είτε τραβώντας την κλωστή μέσα του, ή κρατώντας το απ’ τις δύο άκρες και σπρώχνοντας το ολόκληρο προς τα κάτω. Έστω, τώρα, μια κλωστή που την κρατάμε κι απ’ τις δύο άκρες με τα χέρια μας και την πιέζουμε προς τα κάτω, κάθετα προς το φύλλο κεριού. Εάν η κλωστή είναι κάθετη προς το φύλλο, τότε απλά θα το διαπεράσει ∙ αν, όμως, η κλωστή κρατιέται σε μια θέση, και τεντώνεται λοξά προς το φύλλο, ενώ τα χέρια κινούνται κάθετα προς τα κάτω, τότε η κλωστή, αν είναι γερή, θα δημιουργήσει μια σχισμή στο φύλλο.
Εάν, τώρα, το φύλλο κεριού είχε την ικανότητα να κλείνει πίσω από την κλωστή, αυτό που θα φαινόταν στο χαρτί θα ήταν μια κινούμενη τρύπα.
Έστω, περαιτέρω, ότι αντί για το φύλλο και την κλωστή, έχουμε μια ευθεία γραμμή κι ένα επίπεδο. Εάν η ευθεία γραμμή τοποθετηθεί λοξά προς το επίπεδο και πιεστεί προς τα κάτω, πάντα θα κόβει το επίπεδο σ’ ένα σημείο, αλλά το σημείο τομής θα μετακινούνταν. Εάν το επίπεδο ήταν τέτοιο που να έκλεινε πίσω από τη γραμμή, εάν ήταν φερ’ ειπείν υγρό, θα παρατηρούσαμε, πάνω στο επίπεδο, ένα κινούμενο σημείο. Εάν, τώρα, υπήρχε ένα ολόκληρο σύστημα γραμμών που θα έκλιναν προς διαφορετικές κατευθύνσεις, αλλά που θα συνδέονταν όλες μεταξύ τους και θα παρέμεναν τελείως ακίνητες χάρη σ’ ένα πλαίσιο, κι αν αυτό το πλαίσιο με το σύστημα γραμμών διέσχιζε αργά το υγρό επίπεδο σε ορθογώνια κλίση προς αυτό, θα βλέπαμε να σχηματίζεται μια πληθώρα κινούμενων σημείων στο επίπεδο, ίσες σε αριθμό με τις ευθείες γραμμές στο σύστημα. Οι γραμμές στο πλαίσιο θα κινούνται με την ίδια ταχύτητα – που θα ισοδυναμεί με την ταχύτητα του πλαισίου στο οποίο είναι στερεωμένες. Παρ’ όλα αυτά, τα σημεία στο επίπεδο θα έχουν διαφορετικές ταχύτητες: θα κινούνται είτε ταχύτερα, είτε βραδύτερα, ανάλογα με το πόσο μεγαλύτερη ή μικρότερη θα είναι κλίση που θα έχουν οι γραμμές – από τις οποίες προκύπτουν τα σημεία – προς το επίπεδο. Μια ευθεία γραμμή κάθετη προς το επίπεδο θα δώσει, κατά τη διέλευση της, ένα στατικό σημείο. Μια άλλη ευθεία γραμμή με πολλή μεγάλη κλίση προς το επίπεδο θα δώσει ένα σημείο που θα κινείται με μεγάλη ταχύτητα. Οι κινήσεις και τα μονοπάτια που θα χαράσσουν τα σημεία θα καθορίζονται από τη διάταξη των γραμμών στο σύστημα. Είναι ευνόητο ότι αν δύο ευθείες γραμμές τοποθετούνταν η μία διαγώνια επί της άλλης, όπως το γράμμα Χ, κι ότι αν το σχήμα αυτό στεκόταν όρθιο και διέσχιζε το επίπεδο, αυτό που θα φαινόταν αρχικά θα ήταν δύο σημεία. Τα σημεία αυτά θα πλησίαζαν το ένα το άλλο. Όταν το σημείο όπου οι δύο κάθετες συναντώνται εισερχόταν στο επίπεδο, τα δύο σημεία θα γινόντουσαν ένα ∙ και καθώς το άνω τμήμα του σχήματος θα διέσχιζε το επίπεδο, τα δύο σημεία θα απομακρύνονταν το ένα από το άλλο.
Εάν η γραμμή, με τη σειρά της, θεωρηθεί ως προσαρτημένη σε όλα τα τμήματα του πλαισίου, ενώ ταυτόχρονα τυλίγεται γύρω τους και τα στηρίζει (πλαίσιο ΑΒΓΔ, με συνδεδεμένες τις γραμμές Χ και Υ), τότε τα τμήματα θα μπορούσαν να δημιουργήσουν κάθε είδους σχήματα, και τα σημεία στο επίπεδο θα κινούνταν σε εξαιρετικά περίπλοκα μονοπάτια. Το σχήμα 4 αναπαριστά μια τομή ενός πλαισίου όπως το παραπάνω, με δύο γραμμές ΧΧ και ΥΥ, μολονότι υποτίθεται ότι υπάρχει κι ένας πολύ μεγαλύτερος αριθμός από άλλες γραμμές που κλίνουν προς τα εμπρός και προς τα πίσω, καθώς και προς τα πλάγια.
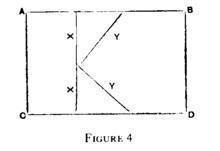
Σύμφωνα με την συνθήκη της σταθερότητας, καμία εκ των κηλίδων αυτών δεν δύναται να παύσει ξαφνικά να υπάρχει. Με άλλα λόγια, η κλωστή, που προκαλεί τη δημιουργία του κινούμενου σημείου μοιραζόμενη την γενική κίνηση του συστήματος, δεν θα πρέπει να σπάσει πριν από τις υπόλοιπες. Εάν όλες οι γραμμές έπαυαν ξαφνικά να υπάρχουν, η κατάσταση αυτή θα αντιστοιχούσε σε εξάλειψη της ύλης.
2. Αδιαπερατότητα: Μία κηλίδα δεν δύναται να περάσει μέσα από μία άλλη. Η συνθήκη αυτή πληρείται πέραν πάσης αμφιβολίας. Εάν οι κλωστές δεν συμπίπτουν σε κανένα σημείο, τότε δεν συμπίπτουν ούτε και οι κινούμενες κηλίδες που προκύπτουν από τις κλωστές.
3. Αδράνεια: Μία κηλίδα δεν θα διακόπτει την κίνηση της, ούτε θα διακόπτει την κατάσταση ηρεμίας της, δίχως να έρχεται σε σύγκρουση με ένα άλλο σημείο. Από τη συνθήκη αυτή προκύπτει μια ακόμη ευνόητη συνθήκη, αυτή τη φορά σχετικά με τις κλωστές: ότι, δηλαδή, αυτές πρέπει να είναι ευθείες στο διάστημα μεταξύ των σημείων όπου έρχονται σε επαφή η μία με την άλλη. Μια κυρτή κλωστή, καθώς διασχίζει το επίπεδο, θα έδινε ένα σημείο του οποίου η ταχύτητα θα μεταβαλλόταν αυθόρμητα – κι αυτό είναι κάτι που ποτέ δεν συμβαίνει με τα σωματίδια της ύλης.
4. Διατήρηση της ενέργειας: Η ενέργεια ενός υλικού συστήματος ποτέ δεν χάνεται ∙ μολονότι δίνει την εντύπωση ότι παύει να υφίσταται, απλά μεταφέρεται από τη μία μορφή στην άλλη. Εάν θεωρήσουμε ότι κάθε μία από τις κινούμενες κηλίδες στο επίπεδο αντιστοιχεί σε μια μονάδα μάζας, τότε, σε κάθε περίπτωση όπου οι κηλίδες αυτές συναντώνται, η αρχή διατήρησης της ενέργειας απαιτεί το άθροισμα των τετραγώνων των μερικών τους ταχυτήτων προτού συναντηθούν, να είναι ίσο με το άθροισμα των τετραγώνων των ταχυτήτων τους αφού συναντηθούν. Έχουμε ήδη δει, όμως, ότι κάθε δήλωση περί της ταχύτητας των κηλίδων στο επίπεδο, δεν είναι παρά μια δήλωση της κλίσης που έχουν οι κλωστές προς το επίπεδο ∙ επομένως, η αρχή διατήρησης της ενέργειας δίνει μια συνθήκη που πρέπει να ικανοποιηθεί από τις κλίσεις των κλωστών του επιπέδου. Μεταφράζοντας την παραπάνω δήλωση με μαθηματικούς όρους, καταλήγουμε στ’ ότι το άθροισμα των τετραγώνων των εφαπτομένων των γωνιών, που σχηματίζουν οι κλωστές με την κάθετο προς το επίπεδο, παραμένει σταθερό.
Ως εκ τούτου, κάθε είδους περιπλοκές και μεταβολές σ’ ένα υλικό σύστημα που αποτελείται από παρόμοια άτομα σ’ ένα επίπεδο θα μπορούσαν να είναι προϊόντα της ομοιόμορφης συνολικής κίνησης ενός συστήματος κλωστών.
Μπορούμε να φανταστούμε τις κλωστές αυτές να πλέκονται η μία με την άλλη για να σχηματίσουν συνδεόμενα σχήματα, το κάθε ένα από αυτά πλήρες από μόνο του, και τα σχήματα αυτά, διασχίζοντας το υγρό επίπεδο, να παράγουν μια σειρά από κινούμενα σημεία. Μολαταύτα, δεδομένου ότι οι κλωστές υποτίθεται ότι σχηματίζουν σταθερά σχήματα, η κίνηση των σημείων δεν θα είναι εξ ολοκλήρου τυχαία, αλλά ορισμένα από αυτά θα φαίνονταν να παίρνουν τη μορφή κινούμενων σχημάτων. Έστω, για παράδειγμα, ένας αριθμός κλωστών συγκεντρωμένος με τρόπο που να σχηματίζει για κάποιο διάστημα έναν κύλινδρο, ο οποίος, όμως, έπειτα από λίγο, ξηλώνεται από τις άλλες κλωστές με τις οποίες διασυνδέονται ∙ καθώς ο κύλινδρος θα διέσχιζε από το επίπεδο, θα προέκυπτε ένας αριθμός σημείων σε έναν κύκλο ∙ όταν το τμήμα στο οποίο οι κλωστές παρεκκλίνουν εισέλθει στο επίπεδο, ο κύκλος θα διαλυθεί επειδή τα σημεία θα απομακρύνονταν. Ως εκ τούτου, τα κινούμενα αυτά σχήματα δεν είναι παρά τα ίχνη των σχημάτων από τις κλωστές, καθώς τα σχήματα αυτά συνεχίζουν το δρόμο τους ∙ και τα κινούμενα αυτά σχήματα θα μπορούσαν να υποτεθούν ότι διαθέτουν ανεξάρτητη ζωή και συνείδηση.
Ή, εάν φαίνεται παράλογο να υποθέσουμε ότι διαθέτουν συνείδηση, αφού τα αρχικά σχήματα, αυτά που τους προσδίδουν το στιγμιαίο ίχνος μορφής, δεν διαθέτουν ένα τέτοιο προσόν, μπορούμε κάλλιστα να θεωρήσουμε ότι η συνείδηση είναι κάτι που κατέχουν τα σχήματα που διαμορφώνονται από τις κλωστές, κι ότι αυτή μοιράζεται από κοινού με τα κινούμενα σχήματα – μόνο που στη δική τους περίπτωση, η συνείδηση τους περιορίζεται στα συγκεκριμένα τμήματα των σχημάτων που διασχίζουν ταυτόχρονα το επίπεδο. Έτσι, μπορούμε να φανταστούμε ότι στο επίπεδο βρίσκονται σώματα που διαθέτουν όλες τις ιδιότητες ενός υλικού συστήματος, σώματα που θα κινούνται και θα μεταβάλλουν τη μορφή τους, και που θα διαθέτουν συνείδηση. Έπειτα από κάποιο χρονικό διάστημα, ένα από τα σώματα αυτά μπορεί να αποσχιστεί από τα υπόλοιπα έτσι που να μην είναι πλέον διακριτό σαν μονάδα ∙ η συνείδηση του, κατά συνέπεια, θα φαίνεται ότι έχει χαθεί. Παρ’ όλα αυτά, οι κλωστές που συγκροτούν την ύπαρξη του δεν σπάνε, ούτε και αλλοιώνεται με οποιοδήποτε τρόπο το αρχικό σχήμα στο οποίο οφείλει την καταγωγή του. Το σχήμα απλά απομακρύνθηκε σε κάποια απόσταση απ’ το επίπεδο. Άρα, τίποτε απ’ όσα υφίστανται στον συνειδητό βίο του επιπέδου δεν παύει να υπάρχει. Μια ύπαρξη όπως αυτή δεν περιλαμβάνει ούτε αιτία, ούτε και αιτιατό – το μόνο που υφίσταται είναι η σταδιακή πραγμάτωση σε μια επιφάνεια ενός ήδη υπαρκτού συνόλου. Η ύπαρξη δεν χαρακτηρίζεται ούτε από την έννοια της προόδου – εκτός κι αν υποθέσουμε ότι οι κλωστές, κατά τη διέλευση τους, πλέκονται μεταξύ τους έτσι που να διαμορφώνουν ακόμη πιο περίπλοκα σχήματα.
Μπορεί, άραγε, μια αναπαράσταση όπως η παραπάνω να χρησιμεύσει προκειμένου να αναπαραστήσει μια ύπαρξη στον χώρο όπου κινούμαστε εμείς; Μπορούμε, άραγε, να θεωρήσουμε ότι οι κινήσεις και οι μεταβολές των υλικών αντικειμένων αντιστοιχούν στις τομές που πραγματοποιεί μια τετραδιάστατη ύπαρξη καθώς έρχεται σ’ επαφή με τον τρισδιάστατο χώρο; Μπορεί, άραγε, η συνείδηση μας να χειριστεί το χωρικό περίγραμμα μιας ανώτερης πραγματικότητας;
Δεν χρειάζεται να επισημάνουμε ότι οι σκέψεις που διατυπώθηκαν αναφορικά με τη δυνατότητα παραγωγής ενός συστήματος, τέτοιου που να πληροί τις συνθήκες υλικότητας μέσω της διάβασης κλωστών διαμέσου ενός υγρού επιπέδου, ισχύουν εξίσου και με την περίπτωση της διάβασης μιας τετραδιάστασης ύπαρξης διαμέσου ενός τρισδιάστατου επιπέδου. Θα αντιλαμβανόμασταν ένα οποιοδήποτε τμήμα της πληρέστερης ύπαρξης, καθώς αυτό θα διέσχιζε τον χώρο μας, ως κάτι το εντελώς περιορισμένο. Τίποτε δεν θα μας έκανε να υποψιαστούμε την σταθερότητα που διαθέτει η ύπαρξη του. Εάν βαδίσουμε στην οδό του παραπάνω συλλογισμού, θα πρέπει να φέρουμε στο νου μας μια ολότητα ασύλληπτου μεγέθους, που μέσα της θα συνυπάρχουν κάθε τι που υπήρξε και κάθε τι που θα υπάρξει, η οποία, καθώς θα διασχίζει αργά τον χώρο μας, θα κληροδοτεί στην δική μας κλονιζόμενη συνείδηση, που τα όρια της δεν υπερβαίνουν έναν στενό χώρο και μία μόνο στιγμή, μια ταραχώδη αποτύπωση μεταβολών και μεταστροφών, που μόνο ο νους μας θα μπορεί να καταγράψει ∙ γιατί το μόνο που θα βλέπαμε θα ήταν μεταβολή και κίνηση. Παρ’ όλα αυτά, τα φαινόμενα αυτά θα δεν ήταν παρά το αποτέλεσμα της στιγμιαίας διέλευσης υπαρκτών πραγματικοτήτων, αέναων και σταθερών, διαμέσου της συνείδησης μας.
Αναλογιζόμενοι τα παραπάνω ζητήματα, δύσκολα μπορούμε να παραμερίσουμε τη συνήθεια να επιζητούμε οπτική ή χειροπιαστή παρουσίαση. Εάν προσπαθήσουμε να σκεφτούμε έναν άνθρωπο που θα υπάρχει σε τέσσερις διαστάσεις, δύσκολα θα αποφεύγαμε να δούμε νοερά τη μορφή του να προεκτείνεται σε μια ήδη οικεία προς εμάς διάσταση. Η εικόνα που σχηματίζουμε με το νου μας, φέρνει κάπως προς εκείνα τα επιβλητικά Αιγυπτιακά αγάλματα, που από μπροστά απεικονίζουν μια αξιοπρεπή καθισμένη φιγούρα, που όμως είναι έως τ’ αυτιά πλαισιωμένη από μια απαλή πέτρινη μάζα που καλύπτει επακριβώς το περίγραμμα της.
Καμιά υλική εικόνα δεν θα μας εξυπηρετήσει. Τα οργανωμένα όντα μας φαίνονται τόσο πλήρη, έτσι που κάθε προσθήκη σε αυτά θα διέφθειρε την ομορφιά τους. Ωστόσο, αν ήμασταν πλάσματα αποκλεισμένα σε ένα επίπεδο, είναι πολύ πιθανό το περίγραμμα ενός Κορινθιακού κίονα να μας φάνταζε τόσο όμορφο που να αποκλείει κάθε απόπειρα βελτιώσεως της μορφής του ∙ θα αδυνατούσαμε να συλλάβουμε την παραμικρή προσθήκης στον κίονα, μόνο και μόνο επειδή κάθε προσθήκη θα κατέληγε να επιθέτει μια άσχημη οπτικά προέκταση σε κάποιο τμήμα του περιγράμματος του. Κινούμενοι στον χώρο των τριών διαστάσεων, όμως, βλέπουμε ότι η ομορφιά του μεγαλοπρεπή κίονα ξεπερνάει κατά πολύ την ομορφιά οποιουδήποτε επιμέρους περιγράμματος. Συνεπώς, το μόνο που μας μένει να κάνουμε είναι να αρνηθούμε στη λογική μας να καταλήξει σε μια ιδανική πληρότητα των μορφών σε τέσσερις διαστάσεις.
Ας αφήσουμε τώρα την προηγούμενη υπόθεση περί πλαισίου και κλωστών, κι ας εξετάσουμε την ιδέα μιας τετραδιάστατης ύπαρξης με τρόπο πιο απλό, και πιο φυσικό – με τον τρόπο, δηλαδή, που ένα δισδιάστατο πλάσμα θα συλλογιζόταν εμάς: όχι ως άπειρα όντα στην τρίτη διάσταση, αλλά ως όντα εξίσου περιορισμένα σε τρεις διστάσεις, όπως κι εκείνο σε δύο. Έτσι, υποθέτουμε ότι ένα ον που ζει σε τέσσερις διαστάσεις θα συναντάει φραγμούς προς τις τέσσερις κατευθύνσεις των διαστάσεων, με την ίδια αναλογία που εμείς φρασσόμαστε από τις τρεις. Το μόνο που μπορούμε να δηλώσουμε αναφορικά με την πιθανότητα ύπαρξης τέτοιων όντων είναι ότι εμείς δεν διαθέτουμε καμία εμπειρία κίνησης προς τέσσερις κατευθύνσεις. Οι δυνάμεις και οι εμπειρίες που θα έχουν τα όντα αυτά θα είναι μεν πιο εκτενείς, αλλά δεν θα παρουσιάζουν θεμελιώδεις διαφορές ως προς τους νόμους της δύναμης και της κίνησης.
Ένα ον τέτοιο θα καθιστούσε ορατό προς εμάς μοναχά ένα μέρος του, αφού ένα δισδιάστατο ον θα αντιλαμβανόταν κάποιον κύβο ως το τετράγωνο επί του οποίου στηρίζεται. Επομένως, ένα τετραδιάστατο ον θα έκανε την εμφάνιση του ξαφνικά ως πλήρες και πεπερασμένο σώμα, κι έπειτα – εξίσου έξαφνα – θα εξαφανιζόταν, δίχως ν’ αφήσει κανένα ίχνος του στον χώρο, όπως θα συνέβαινε στην περίπτωση που κάτι που ακουμπάει σε μια επίπεδη επιφάνεια: εάν υψωνόταν, θα εξαφανιζόταν από το οπτικό πεδίο των όντων, των οποίων η συνείδηση περιορίζεται στο επίπεδο ∙ δεν θα εξαφανιζόταν κινούμενο προς κάποια κατεύθυνση, αλλά θα εξαφανιζόταν ολόκληρο, μονομιάς. Κανένα εμπόδιο, ούτε και κάποιο ανθρώπινο εφεύρημα εγκλεισμού, δεν θα μπορούσε να εμποδίσει το πέρασμα του. Το ον θα διέθετε την ικανότητα να έρχεται και να φεύγει κατά βούληση, πραγματοποιώντας κάθε λογής κατορθώματα που θα αιφνιδίαζαν τον νου. Ο χώρος μας θα μπορούσε – υποθετικά – να διαιρεθεί σε δύο μεριές, εντελώς χωριστές η μία με την άλλη, μέσω ενός άπειρου επιπέδου που θα εκτείνεται προς όλες τις κατευθύνσεις ∙ ένα τετραδιάστατο ον, όμως, θα ξεγλιστρούσε σε όλα τα μέρη του επιπέδου με την μεγαλύτερη δυνατή άνεση.
Για να το δούμε αυτό με μεγαλύτερη σαφήνεια, ας πιάσουμε πρώτα την ανάλογη περίπτωση σε τρεις διαστάσεις: έστω ότι ένα κομμάτι χαρτί αναπαριστά ένα επίπεδο. Εάν το επίπεδο εκτείνεται απείρως προς κάθε κατεύθυνση, τότε θα αναπαριστά ένα άπειρο επίπεδο. Μπορεί να διαιρεθεί σε δύο μέρη από μια άπειρη ευθεία γραμμή. Ένα ον που περιορίζεται σε αυτό το επίπεδο δεν θα μπορεί να μεταβεί από το ένα μέρος στο άλλο δίχως να διασχίσει αυτή τη γραμμή. Έστω, όμως, ότι ένα άλλο κομμάτι χαρτί επικάθεται στο πρώτο και εκτείνεται στο άπειρο ∙ με παρόμοιο τρόπο, το νέο κομμάτι χαρτί θα αναπαριστά ένα άλλο άπειρο επίπεδο. Εάν το ον κινηθεί από το πρώτο επίπεδο μέσω μια κίνησης της τρίτης διάστασης, θα μετακινηθεί στο νέο επίπεδο – και σ’ αυτό δεν θα συναντήσει καμία γραμμή. Έστω ότι το ον κινείται προς μια θέση, τέτοια που όταν θα επιστρέψει στο πρώτο επίπεδο, θα βρεθεί στην άλλη μεριά της γραμμής. Έπειτα, ας επιστρέψει πίσω στο αρχικό επίπεδο. Στην επιστροφή του, θα εμφανιστεί στην άλλη μεριά της γραμμής που διαιρεί το άπειρο επίπεδο σε δύο μέρη.
Ας πάμε τώρα στην περίπτωση των τεσσάρων διαστάσεων. Αντί να φέρνουμε στο νου μας ένα φύλλο χαρτί, ας φανταστούμε ένα στερεό τριών διαστάσεων. Εάν το στερεό καταστεί άπειρο, θα γεμίσει το σύνολο του τρισδιάστατου χώρου. Δεν θα γεμίσει, όμως, το σύνολο του τετραδιάστατου χώρου ∙ θα ήταν, για τον τετραδιάστατο χώρο, ότι είναι κι ένα άπειρο επίπεδο για τον τρισδιάστατο χώρο. Ο τετραδιάστατος χώρος θα μπορούσε να εμπεριέχει έναν άπειρο αριθμό τέτοιων στερεών, όπως ακριβώς θα μπορούσε να εμπεριέχεται ένας άπειρος αριθμός από άπειρα επίπεδα στον τρισδιάστατο χώρο.
Επομένως, δίπλα στον δικό μας χώρο, θα μπορούσε υποθετικά να υπάρχει ένας χώρος που να είναι εξίσου άπειρος προς όλες τις τρεις κατευθύνσεις. Η μετάβαση από τον έναν χώρο στον άλλο απαιτεί μια κίνηση στην τέταρτη διάσταση, με τρόπο παρόμοιο που για να μεταβούμε από το ένα άπειρο επίπεδο στο άλλο, η κίνηση μας οφείλει να είναι στην τρίτη διάσταση.
Φανταστείτε, ομοίως – όπως και με το αρχικό φύλλο χαρτί που αναφέραμε πιο πριν – ένα στερεό ∙ όπως το φύλλο χαρτί υποτίθεται ότι διαθέτει άπειρη έκταση στις δύο διαστάσεις, ας υποθέσουμε ότι το στερεό διαθέτει άπειρη έκταση στις τρεις του διαστάσεις, έτσι που να καταλαμβάνει το σύνολο του αντιληπτού από εμάς χώρου.
Διαιρέστε, στη συνέχεια, το άπειρο στερεό σε δύο τμήματα μέσω ενός απείρου επιπέδου, όπως ακριβώς το άπειρο επίπεδο του χαρτιού διαιρέθηκε σε δύο τμήματα από μία άπειρη γραμμή. Ένα ον δεν μπορεί να μεταβεί από το ένα τμήμα του άπειρου στερεού στο άλλο, που βρίσκεται στην άλλη πλευρά του απείρου επιπέδου, χωρίς την προϋπόθεση να διασχίσει το άπειρο επίπεδο, για όσο τουλάχιστον το ον εξακολουθεί να βρίσκεται εντός του απείρου στερεού.
Υποθέστε, όμως, ότι πλάι σ’ αυτό το άπειρο στερεό βρίσκεται ένα δεύτερο άπειρο στερεό, που είναι στην τέταρτη διάσταση, όπως ακριβώς το δεύτερο φύλλο χαρτί ήταν πλάι στο πρώτο άπειρο επίπεδο στην τρίτη διάσταση. Έστω, τώρα, ότι το ον που έψαχνε να βρει τρόπο να φτάσει στην άλλη πλευρά του διαχωριστικού επιπέδου διαθέτει πλέον την ικανότητα να μετακινηθεί προς την τέταρτη διάσταση, και να εισέλθει στο δεύτερο άπειρο στερεό. Στο δεύτερο στερεό δεν υπάρχει διαχωριστικό επίπεδο. Έστω, λοιπόν, ότι το ον μετακινείται έτσι που όταν θα επιστρέψει στο αρχικό άπειρο στερεό, θα βρει τον εαυτό του στην άλλη πλευρά του άπειρου επιπέδου που το διαιρεί σε δύο τμήματα. Εάν γίνει αυτό, τότε θα βρεθεί στην άλλη πλευρά του απείρου επιπέδου, χωρίς να έχει αναγκαστεί να το διασχίσει.
Με παρόμοιο τρόπο, ένα ον με την ικανότητα να κινείται σε τέσσερις διαστάσεις, θα μπορούσε να βγει από ένα κλειστό κιβώτιο δίχως να περάσει μέσα από τα πλαϊνά του κιβωτίου, διότι θα μπορούσε να μετατοπίσει τον εαυτό του μέσω της τέταρτης διάστασης και να κινηθεί ελεύθερα, έτσι που όταν επιστρέψει, θα βρεθεί έξω απ’ το κιβώτιο.
Υπάρχει κάτι, στον γνωστό προς εμάς κόσμο, που να αποτελεί μία έστω ένδειξη της πιθανότητας ύπαρξης σε τέσσερις διαστάσεις; Στο ερώτημα αυτό δεν δύναται να δοθεί μια οριστική απάντηση. Έχει, παρ’ όλα αυτά, ενδιαφέρον να επισημάνουμε πως υπάρχουν ορισμένα γεγονότα που η ανάγνωση του υπό το πρίσμα της θεωρίας περί τεσσάρων διαστάσεων ανοίγει νέες δυνατότητες ερμηνείας.
Για να αποσαφηνίσουμε τί εννοούμε με τον παραπάνω ισχυρισμό: ας υποθέσουμε ότι ο χώρος είναι όντως τετραδιάστατος, κι ότι ο τρισδιάστατος χώρος που αντιλαμβανόμαστε, σ’ αυτό το εκτενέστερο διάστημα, είναι κάτι σαν μια επιφάνεια στον δικό μας χώρο.
Στο εκτενέστερο διάστημα αυτό, θα νιώθαμε όπως νιώθουν τα όντα που περιορίζονται στην επιφάνεια ενός επιπέδου, όταν αντιλαμβάνονται τον δικό μας χώρο. Έστω, ότι όπως στον χώρο μας υπάρχουν πόλοι έλξης που η επιρροή τους ακτινοβολεί προς κάθε κατεύθυνση, το ίδιο υφίσταται και στο εκτενέστερο διάστημα. Μπορούμε να παρατηρήσουμε κάτι στη φύση που να αντιστοιχεί στην επίδραση ενός πόλου έλξης, που βρίσκεται μεν έξω από τον χώρο μας, αλλά που η επίδραση του διαπερνά το σύνολο της ύλης στον χώρο μας; Η επενέργεια του πόλου έλξης δεν θα αντιστοιχούσε σε κίνηση προς κάποια από τις οικείες προς εμάς κατευθύνσεις, αφού δεν βρίσκεται σε καμία από τις κατευθύνσεις που εμείς γνωρίζουμε.
Αντί για τις τέσσερις και τις τρεις διαστάσεις, ας περάσουμε στις τρεις και τις δύο διαστάσεις, αντίστοιχα: ας φανταστούμε μας ένα επίπεδο που κείτεται οριζόντια, και εντός αυτού κάποια πλάσματα που όλες τους οι εμπειρίες περικλείονται στα όρια του. Εάν χυθεί νερό στο παραπάνω επίπεδο, ή έστω κάποιο άλλο υγρό, τα πλάσματα, καθώς θα αντιλαμβανόντουσαν την παρουσία του, θα διαπίστωναν ότι το νερό που χύνεται έχει μια τάση να εξαπλώνεται σ’ ολόκληρο το επίπεδο. Για την ακρίβεια, τα πλάσματα δεν θα το αντιλαμβανόντουσαν καν ως νερό, όχι με την έννοια που του δίνουμε εμείς ∙ για εκείνα, θα έμοιαζε περισσότερο με αέριο. Διότι ένα αέριο, στη δική μας αντίληψη, τείνει να εκτείνεται προς κάθε κατεύθυνση, και βαθμιαία αυξάνεται προκειμένου να καταλάβει όλο τον χώρο, ασκώντας πίεση στα τοιχώματα του σκεύους στο οποίο το περιορίζουμε.
Το υγρό στο επίπεδο θα επεκτείνεται προς όλες τις διαστάσεις που γνωρίζουν τα δισδιάστατα πλάσματα, ενώ ταυτόχρονα θα μικραίνει στην τρίτη διάσταση, ενώ η απόλυτη ποσότητα του θα παραμένει αμετάβλητη. Κατ’ αυτό τον τρόπο, μπορούμε να υποθέσουμε ότι τα αέρια (που, καθώς επεκτείνονται, μεγεθύνονται στις διαστάσεις που γνωρίζουμε) συρρικνώνονται στην τέταρτη διάσταση.
Η αιτία, σε αυτή την περίπτωση, πρέπει να αναζητηθεί σε κάποια ελκτική δύναμη, τέτοια που να ενεργεί στον δικό μας χώρο όπως ενεργεί η δύναμη της βαρύτητας ως προς ένα οριζόντιο επίπεδο.
Μπορούμε, εντούτοις, να υποθέσουμε ότι υπάρχει ένας πόλος έλξης κάπου στην τέταρτη διάσταση, κι ότι τα αέρια – που όπως γνωρίζουμε, δεν είναι παρά υγρά με μεγαλύτερη κινητικότητα – εξαπλώνονται προς κάθε κατεύθυνση χάρη στην επενέργεια του. Η θεώρηση αυτή συνεπικουρείται από το γεγονός ότι δεν υφίσταται καμία απόλυτη οριοθετική γραμμή μεταξύ ενός υγρού κι ενός αερίου – γεγονός που έχει αποδειχθεί πειραματικό. Το ένα μπορεί να μεταβεί στην κατάσταση του άλλου δίχως κάποιο ενδιάμεσο χρονικό διάστημα που στη διάρκεια του να θεωρηθεί ότι συντελέστηκε μια μεταβολή κατάστασης.
Έτσι, μπορούμε να υποθέσουμε ότι η ύλη, όπως εμείς την αντιλαμβανόμαστε, καθώς εκτείνεται σε τρεις διαστάσεις, διαθέτει επίσης κι ένα μικρό ποσοστό πυκνότητας στην τέταρτη διάσταση ∙ ότι, επίσης, τα στερεά είναι εξίσου άκαμπτα στην τέταρτη διάσταση όπως και στην τρίτη ∙ κι ότι τα υγρά είναι υπερβολικά συμπαγή για να εξαπλωθούν στον χώρο, κι αραιώνουν στην τέταρτη διάσταση υπό την επιρροή ενός πόλου έλξης που βρίσκεται εκτός του χώρου μας – παρ’ όλο που τα υγρά, χάρη στην μεγαλύτερη κινητικότητα των σωματιδίων τους, διέπονται από την επενέργεια του πόλου έλξης και εξαπλώνονται στον χώρο υπό την επιρροή του, με τρόπο παρόμοιο που τα υγρά, υπό την επιρροή της βαρύτητας, εξαπλώνονται σ’ ένα επίπεδο.
Συνεπώς, η πυκνότητα ενός αερίου θα υπολογιζόταν βάσει της σχετικής πυκνότητας που έχει στην τέταρτη διάσταση – και η ελάττωση της πυκνότητας του θα αντιστοιχούσε σε μια ελάττωση της πυκνότητας στην τέταρτη διάσταση. Μπορεί, όμως, ο ισχυρισμός αυτός να τεθεί υπό κάποιου είδους δοκιμή;
Έστω, ένα ον που περιορίζεται σ’ ένα επίπεδο: εάν το επίπεδο απομακρυνθεί πολύ μακριά από τον πόλο έλξης που βρίσκεται έξω από αυτό, τότε το ον θα διαπίστωνε ότι τα υγρά παρουσιάζουν μικρότερη τάση να εξαπλώνονται έναντι της προηγούμενης κατάστασης.
Ή, έστω ότι το ον μετακινείται σ’ ένα μακρινό τμήμα του επιπέδου, τέτοιο που η γραμμή από την θέση του όντος προς τον πόλο έλξης να κείτεται λοξά προς το επίπεδο. Τότε, το ον θα διαπίστωνε ότι σ’ αυτή τη θέση, το υγρό παρουσιάζει μια τάση να εξαπλώνεται περισσότερο προς μία κατεύθυνση έναντι προς την άλλη.
Ας σκεφτούμε τώρα ότι ο χώρος μας, ως κείμενος σε διάστημα τεσσάρων διαστάσεων – όπως ένα επίπεδο στον τρισδιάστατο χώρο –, μπορεί να μετατοπιστεί, κι ότι η επεκτατική δύναμη των αερίων θα φαίνεται, ακολούθως, να διαφέρει σε διαφορετικές περιόδους του χρόνου, ή ότι κατά τη μετατόπιση – όπως συμβαίνει με τη δική μας θέση στον χώρο κατά την πορεία της Γης γύρω από τον ήλιο – ενδέχεται να προκύψει μια επαρκής διαφορά ως προς θέση τη θέση που έχουμε στον χώρο αναφορικά με τον ελκτικό πόλο, έτσι ώστε η δύναμη διαστολής των αερίων να είναι διαφορετική σε διαφορετικές χρονικές περιόδους του έτους, ή αλλιώς, να κάνει τα αέρια να εκδηλώνουν μεγαλύτερη δύναμη διαστολής προς μία κατεύθυνση έναντι μίας άλλης.
Μολονότι ο παραπάνω ισχυρισμός δύναται να επιλυθεί έως κάποιο σημείο, δύσκολα θα θεωρούσαμε ότι επιτρέπει μια οριστική δοκιμή που να αποδεικνύει την φυσική ύπαρξη μιας τέταρτης διάστασης – ούτε, εξάλλου, έχει βρεθεί κάποια δοκιμή που να είναι καθοριστική. Κι είναι αλήθεια πως μένει ένα θεωρητικό ζήτημα μείζονος σημασίας προτού ξεκινήσουμε να αναζητούμε τρόπους δοκιμής: κατά την διερεύνηση των γεωμετρικών ιδιοτήτων που διαθέτουν οι ευθείες γραμμές και τα επίπεδα, υποθέτουμε ότι αυτά αντιστοιχούν σε μία και σε δύο διαστάσεις αντίστοιχα, παρ’ ότι βάσει των προϋποθέσεων αυτών, αρνούμαστε το ενδεχόμενο να έχουν κάποια πραγματική ύπαρξη. Διότι το επίπεδο και η γραμμή δεν είναι παρά αφηρημένες έννοιες, και κάθε τμήμα ύλης διαθέτει τρεις διαστάσεις. Εάν θεωρήσουμε ότι τα όντα του επίπεδου αντιστοιχούν σε κάτι πέραν των ιδεατών μορφών και τίποτε παραπάνω, τότε οφείλουμε αναγκαστικά να υποθέσουμε ότι διαθέτουν ένα κάποιο πάχος. Εάν η εμπειρία των όντων αυτών περιορίζεται στο επίπεδο, το πάχος τους θα είναι εξαιρετικά μικρό σε σχέση με τις άλλες τους διαστάσεις. Αν μεταφέρουμε τον ίδιο συλλογισμό την περίπτωση των τεσσάρων διαστάσεων, καταλήγουμε σ’ ένα ιδιαίτερα παράδοξο συμπέρασμα.
Εάν και εφόσον υπάρχει μια τέταρτη διάσταση, τότε δύο είναι οι εναλλακτικές εικασίες ενώπιον μας.
Η πρώτη είναι ότι η ύπαρξη τεσσάρων διαστάσεων σημαίνει ότι η δική μας ύπαρξη αποτελείται από τρεις διαστάσεις και καμία παραπάνω. Η δεύτερη είναι η ύπαρξη μας συνιστάται σε τέσσερις διαστάσεις, αλλά δεν έχουμε συνείδηση της ιδιότητας αυτής. Εάν είμαστε τρισδιάστατα όντα και τίποτε παραπάνω, παρ’ ότι οι διαστάσεις είναι στην πραγματικότητα τέσσερις, τότε όσον αφορά τα όντα που ζουν σε τέσσερις διαστάσεις, η ύπαρξη μας μοιάζει με εκείνη που έχουν τα όντα των γραμμών και των επιπέδων σε σχέση με εμάς – που σημαίνει ότι όσον αφορά το πώς μας αντιλαμβάνονται τα τετραδιάστατα όντα, δεν είμαστε παρά αφηρημένες μορφές. Σε μια τέτοια περίπτωση, υπάρχουμε μόνο στη συνείδηση του όντος που συλλαμβάνει με την αντίληψη του τη μορφή μας, ενώ οι εμπειρίες μας δεν αποτελούν παρά αντανακλάσεις των σκέψεων που κάνει ο νους του. Αυτό αποτελεί ένα παρόμοιο συμπέρασμα μ’ ένα στο οποίο κατέληξε, από μόνος του, ένας φιλόσοφος της ιδεαλιστικής τάσης.
Η άλλη εναλλακτική εικασία είναι ότι η ύπαρξη μας όντως αποτελείται από τέσσερις διαστάσεις. Σε μια τέτοια περίπτωση, οι αναλογίες που διαθέτουμε βάσει αυτής της ύπαρξης θα πρέπει να είναι απείρως μικροσκοπικές, γιατί αν δεν ήταν, θα διαθέταμε τη συνείδηση τους. Εάν όντως ισχύει κάτι τέτοιο, η ανακάλυψη της τέταρτης διάστασης πρέπει να αναζητηθεί στα απώτερα σωματίδια της ύλης, μιας και τα μεγέθη των απώτερων σωματιδίων ύλης στις τρεις διαστάσεις είναι εξαιρετικά μικροσκοπικά, επιτρέποντας έτσι τη σύγκριση – κατ’ αναλογία – των μεγεθών με τα μεγέθη σε τέσσερις διαστάσεις.
Οι δυο εναλλακτικές εικασίες που παρέθεσα προηγουμένως βασίζονται στην υπόθεση της πραγματικότητας μιας ύπαρξης τεσσάρων διαστάσεων, και η όποια ισχύ τους θα υφίσταται μόνο όσον αφορά την υπόθεση αυτή.
Αν μη τι άλλο, είναι παράδοξο να επισημαίνουμε πως μπορούμε, κατά τα παραπάνω πρότυπα, να συλλάβουμε με το νου μας μια ύπαρξη σχετική προς αυτή που εμείς απολαμβάνουμε, η οποία όμως δεν δύναται να υφίσταται παρά μόνο ως αφηρημένη έννοια.
Πέραν από το ενδιαφέρον που έχουν οι ενατενίσεις τέτοιου τύπου, δεν πρέπει να παραβλέπουμε την πραγματική τους αξία, κι αυτό διότι μας επιτρέπουν να εκφράσουμε, με κατανοητούς όρους, πράγματα που αδυνατούμε να αποτυπώσουμε σε εικόνες. Μας παρέχουν, κατά κάποιο τρόπο, τη σκαλωσιά, την οποία ο νους μπορεί έπειτα να χρησιμοποιήσει προκειμένου να οικοδομήσει τις ιδέες που συλλαμβάνει. Συν τοις άλλοις, το επιπλέον όφελος στην αναπαραστατική μας ικανότητα είναι εξίσου σπουδαίο.
Πολλές από τις ιδέες και θεωρήσεις της φιλοσοφίας είναι σχεδόν ακατάληπτες λόγω του ότι δεν υπάρχει κάποια φυσική αποτύπωση που να εξυπηρετεί την έκφραση τους. Στην φανταστική φυσική ύπαρξη που περιγράψαμε, μπορούν να αναπαρασταθούν πολλά πράγματα που έχουν γραφεί από φιλοσόφους. Θα μπορούσαμε, λόγου χάρη, να αναπαραστήσουμε δια συμβόλων ένα μεγάλο μέρος από την Ηθική του Σπινόζα, αντλώντας στοιχεία από τις παραστάσεις που αποτυπώσαμε στις προηγούμενες σελίδες.
Κατ’ αυτό τον τρόπο, μπορούμε να διερευνήσουμε ενδελεχώς και να καταλήξουμε σε πλήρως εύλογα συμπεράσματα σχετικά με πράγματα που δεν μπορεί να συλλάβει η φαντασία μας.
Βέβαια, όπως είναι άλλωστε φυσικό, οι ενατενίσεις αυτές δεν παρουσιάζουν κάποιο σημείο άμεσης επαφής με οποιουδήποτε είδους τεκμήριο. Αυτό, όμως, δεν συνιστά λόγο για να τα εγκαταλείψουμε. Η πορεία της γνώσης είναι σαν την ροή ενός μεγάλου ποταμού που διασχίζοντας τους εύφορους κάμπους, συγκεντρώνει επάνω του τα ύδατα από κάθε πεδιάδα. Το ποτάμι μπορεί να ενωθεί με κάποιο ρέμα του βουνού, το οποίο, καθώς διασχίζει με δυσκολία τα άγονα βουνοτόπια, χύνεται με ορμή στο μεγάλο ποτάμι από κάποια απόκρημνη κατάβαση, παρουσιάζοντας, κατά τη στιγμή της ένωσης των δύο υδάτων, το πιο πανέμορφο θέαμα που μπορεί να προσφέρει το σύστημα των ποταμών. Το ρέμα δύναται κάλλιστα να χρησιμοποιηθεί προκειμένου να συμβολίσει μία γραμμή μαθηματικής σκέψης, η οποία, καθώς διέρχεται από δύσβατες και αφηρημένες περιοχές, θυσιάζει, για χάρη της κρυστάλλινης σαφήνειας, τον πλούτο που εμπεριέχεται στις μελέτες που διαθέτουν πιο απτές αποδείξεις. Η πορεία του ρέματος ενδέχεται να είναι άκαρπη, μιας κι ενδέχεται να μην ενωθεί ποτέ με τα κεντρικά ύδατα της παρατήρησης και του πειραματισμού. Αν όμως καταφέρει να εισέλθει στην μεγάλη ροή της γνώσης, θα προσφέρει, κατά τη στιγμή της ένωσης του, ένα θέαμα μέγιστης πνευματικής ομορφιάς, και θα προσθέσει κάτι το ισχυρό, και κάτι το μυστηριώδες στην συνεχιζόμενη πορεία των υδάτων.